Odhalování příčin jevů v přírodě a ve společnosti je trvalou výzvou pro vědce všech oborů. Rozvoj moderních měřicích a výpočetních technologií jim umožňuje empiricky nalézat vztahy mezi veličinami (proměnnými) popisujícími stav určitého systému, který je předmětem zkoumání. Různé veličiny mohou spolu korelovat, ale jak určit, co je příčinou a co následkem, je složitější.
Graf 1
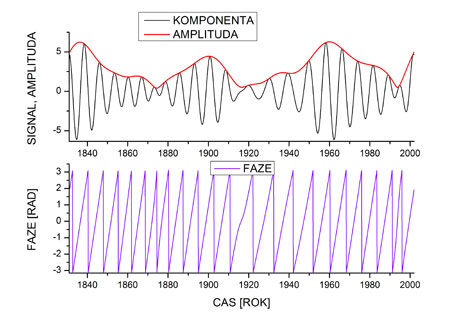
Oscilační komponenta s periodou kolem 7–8 let (černá), její okamžitá amplituda (červená) a okamžitá fáze (fialová).
Mezi různými typy dat, které vědci zaznamenávají a zkoumají, hrají důležitou roli tzv. časové řady. Jde o záznamy hodnot určité veličiny X(t) v po sobě následujících časových okamžicích t = 1, 2, 3… Časová řada představuje digitalizovaný signál, například elektroencefalogram (EEG) – záznam elektrické aktivity mozku. Hodnota napětí mezi dvěma místy na lidské hlavě může být měřena například s frekvencí 1 kHz. V takovém případě znamenají časové okamžiky t = 1, 2, 3… milisekundy a za jednu sekundu tak naměříme tisíc hodnot. Časovou řadu však mohou tvořit i průměrné denní teploty vzduchu, časové oka-mžiky t = 1, 2, 3… představují dny a k získání tisíce hodnot potřebujeme téměř tři roky pozorování. Máme-li zaznamenané dvě časové řady X(t) a Y(t) odrážející vývoj dvou různých veličin, lze se ptát, jaké jsou mezi nimi vztahy a zdali jedna ovlivňuje druhou. Klademe si zásadní otázku o existenci kauzality mezi jevy, jejichž vývoj popisují zkoumané časové řady. Již v roce 1956 se zakladatel kybernetiky Norbert Wiener pokusil formulovat praktický pojem kauzality pomocí vzájemné prediktability signálů: pokud dokážeme předpovědět budoucí hodnotu veličiny X pomocí současných a minulých hodnot veličiny Y lépe než použitím jenom vlastní přítomnosti a minulosti veličiny X, tak Y „kauzálně“ ovlivňuje X. Na úvahy N. Wienera navázal nositel Nobelovy ceny za ekonomii z roku 2003 Clive W. J. Granger, který vyjádřil princip kauzality založený na prediktabilitě prostřednictvím jednoduchých lineárních autoregresních modelů. Termín „Grangerova kauzalita“ označuje matematicky dobře definovaný a měřitelný, číselně kvantifikovatelný vztah orientovaný v čase: příčina předchází následek.
Graf 2
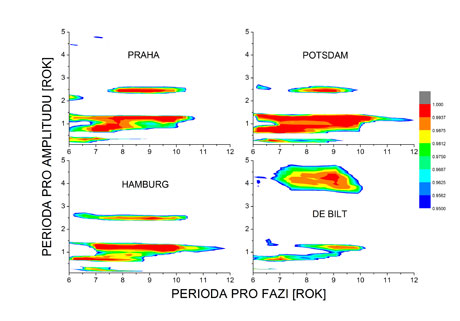
Statisticky významné kauzální působení fáze oscilací s periodou na vodorovné ose na amplitudu variability charakterizované periodou na svislé ose získané pomocí podmíněné vzájemné informace (PVI) z dlouhodobých záznamů průměrných denních teplot v Praze-Klementinu, Postupimi, Hamburku a v holandském De Biltu. Barevně kódované je každé překročení 95. percentilu rozdělení PVI pro nulovou hypotézu žádné mezifrekvenční závislosti.
Studium interakcí ve složitých nelineárních systémech vyžaduje zobecnění matematického aparátu Grangerovy kauzality pro nelineární procesy, respektive nelineární časové řady. Navrhli jsme využití nástrojů teorie informace. Neurčitost náhodné veličiny X je charakterizovaná její entropií H(X) způsobem, jak jej navrhl Claude Shannon. Společná entropie dvou veličin H(X, Y) je menší než součet individuálních entropií H(X) + H(Y) jen tehdy, když veličiny X a Y nejsou nezávislé, čili znalost jedné snižuje neurčitost druhé. Množství společné informace v proměnných X a Y charakterizuje vzájemná informace I(X; Y). Tato užitečná míra obecné statistické závislosti je definována právě jako rozdíl I(X; Y) = H(X) + H(Y) – H(X, Y). Závislost dvou veličin X, Y může být někdy vyvolána vlivem třetí veličiny Z. „Čistou“ závislost mezi X a Y, s vyloučením vlivu Z, měříme podmíněnou vzájemnou informací I(X; Y|Z), definovanou analogicky pomocí podmíněných entropií.
Jak nyní odhalit možné kauzální vztahy mezi procesy, respektive časovými řadami X(t) a Y(t)? Vzájemná informace I(X(t); Y(t + τ)) měří množství společné informace, neboli závislost mezi procesem X v současnosti (čas t) a procesem Y v budoucnosti (čas t + τ). Tato míra však nevyjadřuje kauzální působení X(t) na Y(t + τ), nýbrž obsahuje i informaci danou společnou historií, čili závislostí mezi X(t) a Y(t). Kauzální působení X(t) na Y(t + τ) měří podmíněná vzájemná informace I(X(t);Y(t + τ)| Y(t)). Je nutné, aby závislost mezi X(t) a Y(t + τ) byla podmíněná úplným určením současného stavu procesu Y, což v reprezentaci časových řad znamená vektor složený ze současnosti Y(t) a určitého počtu kroků do minulosti Y(t – 1), Y(t – 2)… Ukázali jsme, že takto definovaná podmíněná vzájemná informace je, ve spolupráci s vhodným statistickým testem, schopna odhalit kauzální vztahy mezi nelineárními procesy. Tento přístup jsme použili ve studiích kauzálních vztahů mezi rytmy srdce a dýchání a k detekci informačních toků (kauzálního působení) ve směru od epileptického ložiska do okolních částí mozku v EEG signálech epileptiků.
Graf 3
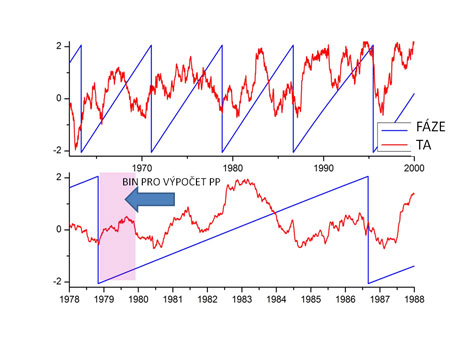
Fáze osmiletého cyklu (modrá) a shlazené teplotní anomálie z Prahy-Klementina (červená) se schematickým vyznačením fázového binu pro výpočet podmíněných průměrů teplotních anomálií
Problém detekce kauzálních vztahů se přirozeně objevuje ve studiích dvou a více procesů. V nejnovější práci jsme se zaměřili na jeden proces s komplikovanou dynamikou probíhající současně v různých časových škálách. Je známo, že například EEG obsahuje vlny, přesněji oscilace různých frekvencí, označované jako delta, teta, alfa, beta, gama. Dlouhodobé záznamy přízemních teplot vzduchu obsahují krátkodobou variabilitu počasí, sezonní změny, dlouhodobou variabilitu a změny klimatu. Existují matematické a výpočetní metody, jak takovou složitou dynamiku v různých časových měřítkách rozdělit na (kvazi)oscilační komponenty určitého frekvenčního obsahu. Oscilační dynamiku je vhodné popsat pomocí její okamžité fáze a amplitudy (graf 1). Následně je možné studovat různé typy meziškálových, respektive mezifrekvenčních interakcí. Pomocí odhadů podmíněné vzájemné informace a vhodných statistických testů jsme v dlouhodobých teplotních záznamech odhalili kauzální působení fáze oscilací s periodou mezi 6–11 lety na amplitudy teplotní variability charakterizované časovými škálami několika měsíců až 2–3 let. Konkrétní charakter meziškálových interakcí v teplotních záznamech, a tudíž v dynamice atmosféry závisí na geografické poloze místa měření teplot. Výsledky ze střední Evropy se však vyznačují vysokou robustností a reprodukovatelností (graf 2). Zásadním přínosem studie je kvantitativní důkaz existence nově pozorovaného fyzikálního jevu. K pochopení jeho významu ovšem potřebujeme další informace.

Foto: Stanislava Kyselová, Akademický bulletin
Milan Paluš představuje výstupy své studie: monitor vlevo zobrazuje oblast Evropy s významným vlivem osmiletého cyklu na teplotní variabilitu; vpravo výsledky testu kauzálních meziškálových interakcí v dynamice atmosféry pro jiné evropské lokality (analogie grafu 2).
Několik nezávislých studií (včetně starší práce autora ve spolupráci s Dagmar Novotnou z Ústavu fyziky atmosféry AV ČR) založených na analýzách záznamů teplot a dalších meteorologických veličin potvrdilo existenci nepravidelných klimatických oscilací s periodou fluktuující v rozsahu 6–11 let, nejčastěji však nabývající hodnotu 7–8 let. Jelikož amplituda těchto oscilací není velká, klimatologové jim nevěnovali pozornost. Meziškálové interakce však zesilují jejich vliv na teplotní variabilitu. Kvůli odhadu velikosti tohoto vlivu jsme extrahovali okamžitou fázi oscilace s periodou přibližně osm let z dlouhodobého teplotního záznamu z Prahy-Klementina (graf 3). Rozdělili jsme hodnoty fáze do osmi binů a v každém binu ve všech osmiletých cyklech spočetli průměrnou hodnotu teplotních anomálií (TA). TA jsou odchylky teplot od dlouhodobých sezonních průměrů, neboli teplotní záznamy po odstranění ročního cyklu. Tímto způsobem jsme získali podmíněné průměry TA, tj. podmíněné hodnotou fáze osmiletého cyklu čili polohou konkrétního data relativně k určitému osmiletému cyklu. Pokud osmiletý cyklus nemá vliv na variabilitu teplot v Praze, podmíněné průměry by neměly na fázi cyklu záviset; měly by být asymptoticky stejné. Průměry přes omezený záznam stejné nebudou, ale měly by fluktuovat nezávisle na hodnotě fáze osmiletého cyklu. Jaká je skutečnost, ukazuje graf. 4. Podmíněné průměry jasně ukazují cyklický průběh a rozdíl mezi minimem a maximem teplotní anomálie během cyklu je přibližně 1,5 °C. Zjednodušeně můžeme říct, že vliv přibližně osmiletého cyklu na meziroční variabilitu teplot činí podle pražských záznamů průměrně 1,5 °C. V některých oblastech Německa a Polska dosahuje tato hodnota 2 °C.
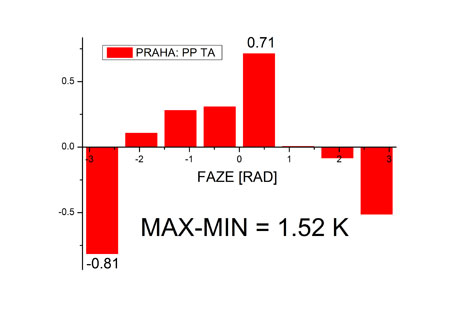
Graf 4
Podmíněné průměry teplotních anomálií pro Prahu-Klementinum podmiňované hodnotou fáze osmiletého cyklu, počítané pro období 1958–2002
Matematický aparát teorie informace a principu Grangerovy kauzality nám pomohl odhalit meziškálové interakce v dynamice atmosféry, konkrétně vliv pomalejších nepravidelných cyklů na krátkodobou variabilitu teploty. Jednoduché výpočty podmíněných teplotních průměrů ukázaly, že tento efekt je nezanedbatelný. Bude potřeba další výzkum k pochopení fyzikálních mechanismů meziškálových interakcí, vytvoření jejich počítačových modelů, které v budoucnu poskytnou nové možnosti predikce teplotní variability v různých časových škálách. Jde o složitý problém, do něhož pravděpodobně vstupují ještě pomalejší procesy (například Atlantická multidekadální oscilace) a samozřejmě dlouhodobé trendy v důsledku globální změny klimatu.
Další literatura: Paluš, M., Multiscale atmospheric dynamics: Cross-frequency phase-amplitude coupling in the air temperature. Phys. Rev. Lett. 112 (2014) 078702. Paluš, M. – Vejmelka, M., Directionality of coupling from bivariate time series: How to avoid false causalities and missed connections. Phys. Rev. E 75 (2007) 056211. Hlaváčková-Schindler, K. – Paluš, M. – Vejmelka, M., Bhattacharya, J., Causality detection based on information-theoretic approaches in time series analysis. Phys. Rep. 441 (2007) 1–46. Preprinty na http://www.cs.cas.cz/mp/epr/epr0.html.
MILAN PALUŠ,
Ústav informatiky AV ČR, v. v. i.


 English
English